Sortable Semantic Version Strings in Rails (part 1)
Sometimes we need to sort string values that aren’t lexicographically sortable. For example, a list of Semantic Version strings
like 1.0.0-rc1, 1.2.4, 1.1.0-beta and 2.0.0.
This post describes how these strings can be encoded as a unique integer value that is sortable, using a technique called bit packing.
- Part 1 explains the concept and the constraints of this method
- Part 2 describes how to implement this in ActiveRecord
- Part 3 describes an alternative approach that is SQL driven
Defining the problem
Semantic Version strings aren’t sortable using lexicographical sorting methods. So, a version string like 1.11.0 should come after a version string 1.9.0 when ordered using
Semantic Versioning, but would come before it in an ascending lexicographical sort.
To see this problem in action, try running the following Ruby code in a console:
%w[ 1.10.0 1.9.0 2.4.1 0.123.0 4.0.0-rc1 ].sort
# => ["0.123.0", "1.10.0", "1.9.0", "2.4.1", "4.0.0-rc1"]
Version 1.9.0 should come before 1.10.0 in this list (because 9 is less than 10 😵💫). But comes after, because the strings are compared character by character until a difference appears, and so 1 is compared to 9 and found to be lower.
Sorting records by SemanticVersion as part of a SQL SELECT can be tricky, as well as slower, because we have to apply various functions on each row to split the strings into their component parts (or do a WHERE ... IN (?)) with a set of preselected version numbers.
But what if there was a way to convert our Semantic Version strings into a format that was both sortable and lightning-fast?!
Bit Packing
You probably know that natural numbers can be represented in binary form, and conversely, that binary numbers can be represented as natural numbers. But what if we could store non-numerical information—our Semantic Version string—in an encoded binary form, and then represent that as a unique integer that was sortable by its Semantic Version precedence?
Here’s a simple example to demonstrate the concept…
We can represent integers from zero to 255 using 8 bits of binary. For example, the number 12 can be represented
as: 00001100 (8 + 4 = 12)
| Bit place value | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| State | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
This simple example should hopefully be straightforward—we can store natural numbers as binary. But we’re only using 4 bits of data here, not all 8. Database Integers are typically up to 32-bits, and BigInt types are 64-bits long. What if we were to use more of the available bits as places to store additional information?
Let’s look at a slightly more complicated example. The numbers 15 and 12 could separately be represented as the
following two 4-bit binary representations 1111 and 1100:
| Bit place value | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| State | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| Bit place value | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| State | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 |
But we could join these two separate 4 bit binary values into single 8-bit binary value:
| Bit place value | 128 | 64 | 32 | 16 | 8 | 4 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|
| State | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
Here, we’ve represented the numbers 15 and 12 as the binary number 11111100, which is just 1111 and 1100
concatenated together. The natural number value this binary represents is not 1512 (15 and 12), but 252.
In other words, we have found a way to represent our two numbers in a format that is more compact (252 has fewer digits than 1512 would), is unique to this particular combination of values, and can lexicographically sorted and indexed.
Knowing how these values were stored, we can also decode this value, converting the number 252 back into the binary 11111100; splitting it in two to give 1111 and 1100, and converting these back to integers 15 and 12. In other words, the process is reversible.
Can we use this method to store a whole Semantic Version string as an integer? (hint: yes we can!).
Components of a Semantic Version String
The Semantic Versioning Specification (SemVer) is fairly flexible, and allows for a variety of valid version string formats. The majority of use cases, though, can be boiled down to the following components:
MAJOR.MINOR.PATCH-PRERELEASE+BUILD
- Major version (required). Typically a natural number greater than or equal to zero. Usually, most software projects will have a major version between 0 and 10, but some will go much higher.
- Minor version (required). Typically a natural number greater than or equal to zero. It’s not uncommon for a major version of a software to have dozens of minor releases.
- Patch version (required). Typically a natural number greater than or equal to zero. It’s not uncommon for a minor version of a software to have dozens of minor releases.
- Prerelease label (optional). Something like “alpha”, “beta”, or “rc”. Can often be followed by a prerelease version number.
- Prerelease version (optional). Typically, a natural number greater than zero; commonly lower than 10. Follows the prerelease label, and indicates the nth version for that prerelease type (e.g. beta.2).
- Build metadata (optional). The metadata for the current build. Can hold a variety of alphanumeric data. MUST be ignored when determining version precedence.
So, in the case of a version string: 1.0.2-beta.3+foobar, we can say the major version is 1, the minor version is 0,
the patch version is 2, the prerelease label is beta and the prerelease version is 3, and the build metadata is foobar (but we don’t care about build metadata).
Note that major, minor, and patch are required for a valid SemVer value, whereas everything after that is optional.
Encoding SemVer strings as unique integers
All of this is very interesting, but how can we pack a long string of mixed numbers, text, and symbols, as an incremental integer?
The trick here is to designate specific bit places (or columns) of our 32-bit integer data to specific components of our SemVer string—just like we did with the numbers 15 and 12 above. To do this, we have to agree to some constraints on the version information we allow ourselves to store.
For example, let’s agree that we’re not likely to release more than 100 major versions of our application in its
lifespan? In that case, we can say that the highest major version we will likely store is 99. In binary, 99 is
represented as 1100011. So, we need at least 7 bits to represent the major component of our SemVer string (7 bits actually allows gives us up to 127 major versions).
We will likely release more minor versions, so let’s allow ourselves at least up to 999 minor versions per major
release. 999 is represented as the binary value 1111100111, and so we’ll need at least 10 bits to represent the minor
component of our SemVer string.
We can repeat this for patch versions, and allow another 10 bits to represent our patch version number.
So far, we could represent any MAJOR.MINOR.PATCH version string using 32 bits like so:
(this table is scrollable)
| Bit place | 32 | 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Represents | MAJOR | MAJOR | MAJOR | MAJOR | MAJOR | MAJOR | MAJOR | MINOR | MINOR | MINOR | MINOR | MINOR | MINOR | MINOR | MINOR | MINOR | MINOR | PATCH | PATCH | PATCH | PATCH | PATCH | PATCH | PATCH | PATCH | PATCH | PATCH | unused | unused | unused | unused | unused |
and still have 5 bits left to spare (we’ll use those later).
So for example, version 8.1.4 could be broken into its constituent parts: 8, 1, and 4.
These are represented in binary as: 1000, 1, and 100, respectively.
ℹ️ You can prove this to yourself by writing
8.to_s(2)in a Ruby console:8.to_s(2) # => "1000"
Since we decided above that we would allocate 7 bits to the major version, and 10 bits each to the minor and patch
versions, we would represent these values fully as 0001000, 0000000001, and 0000000100.
Concatenate them all together, leaving the last 5 bits unset, we have the 32 bit binary
value: 0001000 0000000001 0000000100 00000.
Binary is typically written in 8 bit groups called bytes, so we can adjust the spacing on this
to 00010000 00000000 10000000 10000000.
ALLLLLL of this, is to say that: we can represent the SemVer number 8.1.4 with the binary
value 00010000 00000000 10000000 10000000, which is equal to the integer 268468352. This number is unique to this
SemVer value.
ℹ️ You can prove this to yourself by writing
0b00010000_00000000_10000000_10000000in a Ruby console:0b00010000_00000000_10000000_10000000 # => 268468352
So far, so good?
Including the prerelease type
Remember the unused bits in the previous section? We’re going to put them to good use now…
Since SemVer includes the option to have prereleases, such as alpha1 or rc.2, we ought to add some support for these too. To do so, we have to again commit ourselves to some reasonable constraints.
In this case, the constraints are that we should have a limited number of prerelease types that we may use: say (alpha, beta, rc) and assume that everything else is a release release type. With these four types agreed upon, we can represent each of them using just two bits of binary data.
- alpha
- This comes first in order precedence, and should be represented as
00 - beta
- This comes second in order precedence, and should be represented as
01 - rc
- This comes third in order precedence, and should be represented as
10 - release
- This comes last in order precedence, and should be represented as
11
Now, we have a two-bit representation for the prerelease type component of our SemVer string that will preserve the proper order precedence when we include it in our long binary number. Let’s update that number, using two of the unused bits from our 32 bit binary number in the previous section.
| Bit place | 32 | 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Represents | MAJOR | MAJOR | MAJOR | MAJOR | MAJOR | MAJOR | MAJOR | MINOR | MINOR | MINOR | MINOR | MINOR | MINOR | MINOR | MINOR | MINOR | MINOR | PATCH | PATCH | PATCH | PATCH | PATCH | PATCH | PATCH | PATCH | PATCH | PATCH | PRERELEASE TYPE | PRERELEASE TYPE | unused | unused | unused |
Now, we could represent the following versions by the these binary values (I’ve added parentheses around the bits that have been changed):
| SemVer | Binary | Integer |
|---|---|---|
8.1.4-alpha |
00010000_00000000_10000000_100(00)000 |
268468352 |
8.1.4-beta |
00010000_00000000_10000000_100(01)000 |
268468360 |
8.1.4-rc |
00010000_00000000_10000000_100(10)000 |
268468368 |
8.1.4 |
00010000_00000000_10000000_100(11)000 |
268468376 |
Storing the prerelease version
We have three unused bits of our 32 bit integer left, and we still don’t have a way of supporting prerelease version numbers (like the 3 in 1.0.0-rc.3). We can store this information in the same way we have stored the major, minor, and patch versions—again, if we accept some reasonable constraints.
Since we have three bits of space left, we can support up to seven numbered prerelease version numbers per prerelease type (alpha7, beta7, or rc7). That’s probably plenty. Encoding these as binary is relatively straightforward, as we don’t have to do anything other than convert the prerelease version number to binary and occupy the first three bits.
Our final mapping of bits to values should look like this:
(again, the table is scrollable)
| Bit place | 32 | 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Represents | MAJOR | MAJOR | MAJOR | MAJOR | MAJOR | MAJOR | MAJOR | MINOR | MINOR | MINOR | MINOR | MINOR | MINOR | MINOR | MINOR | MINOR | MINOR | PATCH | PATCH | PATCH | PATCH | PATCH | PATCH | PATCH | PATCH | PATCH | PATCH | PRERELEASE TYPE | PRERELEASE TYPE | PRERELEASE VERSION | PRERELEASE VERSION | PRERELEASE VERSION |
Let’s look at a complete example of how valid SemVer strings would look as binary and integers using this system (I’ve added parentheses around the bits that have been changed):
| SemVer | Binary | Integer |
|---|---|---|
8.1.4-alpha |
00010000_00000000_10000000_10000(000) |
268468352 |
8.1.4-alpha.1 |
00010000_00000000_10000000_10000(001) |
268468353 |
8.1.4-alpha.2 |
00010000_00000000_10000000_10000(010) |
268468354 |
8.1.4-alpha.3 |
00010000_00000000_10000000_10000(011) |
268468355 |
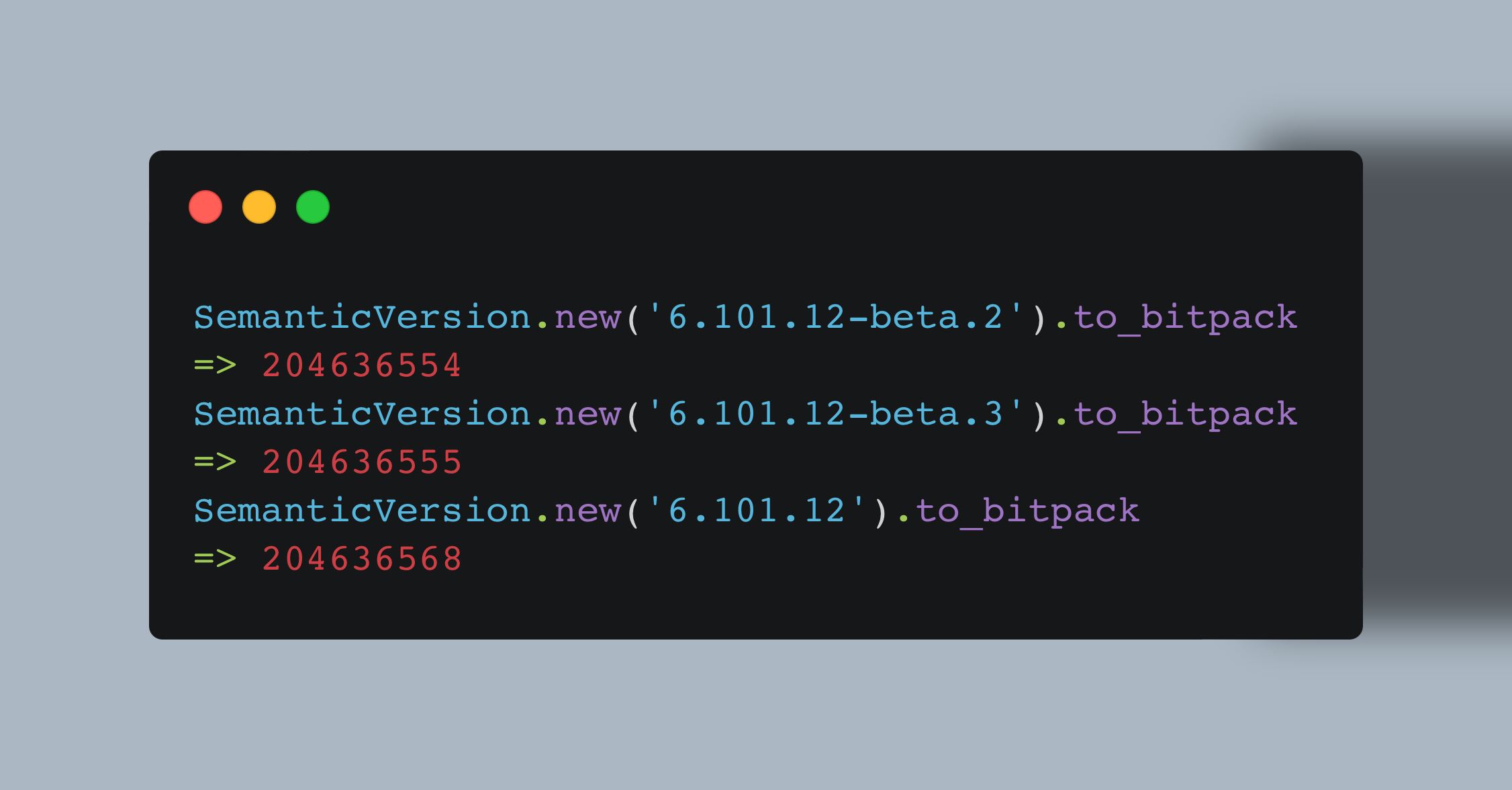
Note that, in this case, the integer values go up sequentially by 1 each time.
Summary
Let’s summarise what we just did.
We took a 32-bit binary value, and separated it into smaller chunks that represent the various components of a valid SemVer string.
Reading from left to right, the first 7 bits represent the major, the next 10 bits represent the minor, and the next 10 the patch. The following 2 bits represent the prerelease type, and the last 3 bits represent the prerelease version number.
To spare you from taking off your socks, 7 + 10 + 10 + 2 + 3 = 32 bits.
A version string like 52.123.12-beta.2 can be broken into:
52=>0110100123=>000111101112=>0000001100beta=>012=>010
Which can all be concatenated together as 0110100 0001111011 0000001100 01 010.
This is the binary representation for 1748861322.
52.123.12-beta.2 can be represented as 1748861322.
In the next section, we’ll look at how we can implement this in an ActiveRecord model.
- Read Part 2 describes how to implement this in ActiveRecord
